All signal processing techniques exploit signal structure; when the signals are random, we want to understand the probabilistic structure of irregular, ill-formed signals. Such signals can be either be bothersome (noise) or information-bearing (discharges of single neurons). Our research is predicated on the notion that a deep understanding of a signal’s structure will result in signal processing algorithms that can either suppress bothersome signals or enhance information-bearing ones. Current research ranges from fundamental studies of non-Gaussian signals and how systems extract and represent information to applying these theories to the analysis of neural data and modeling of how neural structures process information.

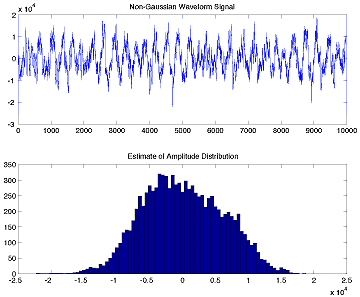
Stationary non-Gaussian signals occur frequently in practical situations. For example, the amplitude distributions of ambient underwater sounds and of background electromagnetic signals have been found to deviate strongly from a Gaussian characterization.

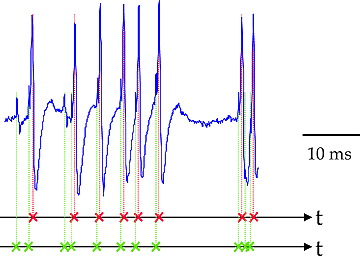
Neural discharges are modeled as stochastic point processes, which have no waveform, thereby disallowing Gaussian models.

Combined discharges of neural populations and DNA sequences represent examples of symbolic data, which have amplitudes selected from a finite set: the signal takes on values drawn from the alphabet representing base pairs {A, C, G, T}. These signals are particularly interesting since amplitudes have no mathematical operations defined for them: No field or group can be meaningfully defined for them. We have found ways of computing the Fourier and wavelet transforms of symbolic signals.